MATEMATIKA KITA: Aplikasi Turunan Fungsi

Ada beberapa penggunaan turunan fungsi, diantaranya terdapat pada :

Persamaan garis singgung
Fungsi naik dan fungsi turun
menggambar grafik fungsi aljabar
Maksimum dan minimum fungsi
Teorema L’Hopital
Nilai stasioner
Titik belok
Kecepatan dan percepatan

Perhatikanlah tabel berikut!

$\begin{array}{|c|c|l|c|}\hline \multicolumn{3}{|c|}{\textrm{Turunan Pertama}}&\textrm{Turunan Kedua}\\\hline 1.&\textrm{\textrm{Gradien garis singgung}}&m={f}\, '(x)=\underset{h\rightarrow 0}{\textrm{Lim}}=\displaystyle \frac{f(x+h)-f(x)}{h}&\textrm{Belok}\\\cline{1-3} 2.&\textrm{Fungsi naik dan turun}&y=f(x)\begin{cases} {f}'(x)> 0, & \text{ fungsi naik } \\ {f}'(x)< 0, & \text{ fungsi turun } \end{cases}&\textrm{Percepatan}\\\cline{1-3} 3.&\textrm{Jarak, kec, percepatan}&y=s(t)\begin{cases} s(t) & \text{ jarak} \\ {s}\, '(t) & \text{ kecepatan } \\ {s}\, ''(t) & \text{ percepatan} \end{cases}&\textrm{Maksimum}\\\cline{1-3} &&\begin{aligned}\textrm{Maksimum}:&\\ \rightarrow {f}&\, ''(k)< 0\\ \textrm{titik mak}&\: \left ( k, f(k)\right ) \end{aligned}&\textrm{Minimum}\\\cline{3-3} 4.&\textrm{Stasioner}&\begin{aligned}\textrm{Minimum}:&\\ \rightarrow {f}&\, ''(k) > 0\\ \textrm{titik min}&\: \left ( k, f(k)\right ) \end{aligned}&\\\cline{3-3} &{f}\, '(x)=0\rightarrow x=k&\begin{aligned}\textrm{Belok}:&\\ \rightarrow {f}&\, ''(k)= 0\\ \textrm{titik belok}&\: \left ( k, f(k)\right ) \end{aligned}&\\\cline{1-3} 5.&\begin{aligned}&\textrm{Limit fungsi}\\ &\textrm{bentuk tak tentu} \end{aligned}&\begin{aligned}&\textrm{Aturan L'Hopital}\\ &\\ &\underset{x\rightarrow h}{\textrm{Lim}}\: \: \displaystyle \frac{f(x)}{g(x)}=\underset{x\rightarrow h}{\textrm{Lim}}\: \: \displaystyle \frac{{f}\, '(x)}{g\,'(x)}\\ &\\ &\textrm{untuk hasil limit}\\ &\textrm{bentuk}\: \: \frac{0}{0}\: \: \textrm{atau}\: \: \frac{\infty }{\infty }\end{aligned}&\\\hline \end{array}$ .

CONTOH PERSOALAN

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah persamaan garis singgung pada kurva}\: \: y=x^{2}+2x-8\: \: \textrm{di titik yang}\\ &\textrm{berabsis}\: \: 1 \end{array}\\\\\\ \textrm{Jawab}:\\\\ \begin{array}{|c|c|l|}\hline \multicolumn{3}{|c|}{\begin{aligned}&\\ \textrm{Diketahui},\: &\textrm{persamaan sebuah kurva adalah:}\\ &y=x^{2}+2x-8\\ & \end{aligned}}\\\hline \textrm{Titik singgung}&\textrm{Gradien}\: ,\: x=1&\textrm{Persamaan garis singgung}\\\hline \begin{aligned}x=1\rightarrow y&=(1)^{2}+2(1)-8\\ &=1+2-8\\ &=-5\\ &\\ \textrm{di titik}&\: \: (a,b)=(1,-5)\end{aligned}&\begin{aligned}\displaystyle \frac{dy}{dx}=m&=2x+2\\ &=2(1)+2\\ &=4\\ &\\ & \end{aligned}&\begin{aligned}y&=m(x-a)+b\\ &=4(x-1)+(-5)\\ &=4x-4-5\\ &=4x-9\\ & \end{aligned}\\\hline \multicolumn{3}{|c|}{\begin{aligned}&\\ \textrm{Jadi},\: &\textrm{persamaan garis singgungnya adalah:}\\ &y=4x-9\Leftrightarrow y-4x+9=0\\ & \end{aligned}}\\\hline \end{array}$ .

Berikut ilustasi gambar dari persoalan di atas

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah interval di mana kurva fungsi}\: \: f(x)=x^{3}+3x^{2}-9x+5\\ &\textrm{a}.\quad \textrm{naik}\\ &\textrm{b}.\quad \textrm{turun} \end{array}\\\\\\ \textrm{Jawab}:\\\\ \begin{array}{|l|l|}\hline \multicolumn{2}{|c|}{\begin{aligned}&\\ f(x)&=x^{3}+3x^{2}-9x+5\\ {f}\, '(x)&=3x^{2}+6x-9\\ &=3(x+3)(x-1)\\ & \end{aligned}}\\\hline \textrm{naik}\: ;\: \: {f}\, '(x)> 0&\textrm{turun}\: ;\: \: {f}\, '(x)< 0\\\hline \begin{aligned}&\\ &3(x+3)(x-1)> 0\\ & \end{aligned}&\begin{aligned}&\\ &3(x+3)(x-1) < 0\\ & \end{aligned}\\\hline \multicolumn{2}{|c|}{\begin{array}{ll|lll|lll}\\ &\multicolumn{3}{c}{.}&\multicolumn{3}{c}{.}&\\\cline{1-2}\cline{6-7} +&+&-&-&-&+&+&\\ &&&&&&\\\hline &\multicolumn{2}{l}{-3}&&\multicolumn{2}{c}{1}&&\\ \end{array} }\\\hline \begin{aligned}&\\ \textrm{naik}\: ,&\: x< -3\: \: \textrm{atau}\: \: x> 1\\ & \end{aligned}&\begin{aligned}&\\ \textrm{turun}\: ,&\: -3< x< 1\\ & \end{aligned}\\\hline \end{array}$ .

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah nilai stasioner fungsi}\: \: f(x)=x^{3}+3x^{2}-9x+5 \: \: \textrm{dan tentukan pula jenisnya}.\end{array}\\\\\\ \textrm{Jawab}:\\\\ \begin{aligned}&\\ f(x)&=x^{3}+3x^{2}-9x+5\\ {f}\, '(x)&=3x^{2}+6x-9\\ &=3(x+3)(x-1)\\ &\textrm{dan}\\ &\begin{array}{ll|lll|lll}\\ &\multicolumn{3}{c}{.}&\multicolumn{3}{c}{.}&\\\cline{1-2}\cline{6-7} +&+&-&-&-&+&+&\\ &&&&&&\\\hline &\multicolumn{2}{l}{-3}&&\multicolumn{2}{c}{1}&&\\ \end{array} \\ &\textrm{untuk nilai stasionernya} \\ f(-3)&=(-3)^{3}+3(-3)^{2}-9(-3)+5=32&\rightarrow \left ( -3,32 \right )\: \textrm{adalah titik balik maksimum}\\ f(1)&=(1)^{3}+3(1)^{2}-9(1)+5=0&\rightarrow \left ( 1,0 \right )\: \textrm{adalah titik balik minimum} \end{aligned}$ .

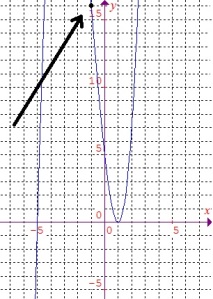
Berikut ilustrasi gambar kurvanya baik untuk jawaban No. 2 maupun No. 3

$\begin{array}{ll}\\ 4.&\textrm{Masih sama dengan soal seperti pada No. sebelumnya, yaitu fungsi}\: \: f(x)=x^3+3x^2-9x+5\: .\\ & \textrm{Tentukanlah koordinat titik beloknya}\end{array}\\\\\\ \textrm{Jawab}:\\\\ \begin{array}{|c|c|c|c|l|c|}\hline \multicolumn{6}{|c|}{\begin{aligned}&\\ f(x)&=x^3+3x^2-9x+5\\ {f}\, '(x)&=3x^{2}+6x-9\\ {f}\, ''(x)&=6x+6\\ \textrm{Proses}\: &\textrm{mencari beloknya}\\ {f}\, ''(x)&=0\\ 6x+6&=0\\ 6x&=-6\\ x&=-1\\ & \end{aligned}}\\\hline \textrm{Interval}&f(x)&{f}\, '(x)&{f}\, ''(x)&\: \: \qquad \textrm{Keterangan}&\textrm{Koordinat titik beloknya}\\\hline x< -1&&&-&\textrm{grafik cekung ke bawah}&\\\cline{1-5} x= -1&16&-12&0&\textrm{grafik memiliki titik belok}&(-1,16)\\\cline{1-5} x > -1&&&+&\textrm{grafik cekung ke atas}&\\\hline \end{array}$ .