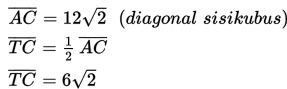Sudut Antara Garis dan Bidang
Garis Sejajar Bidang
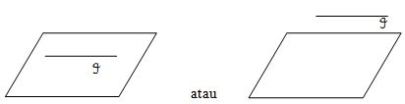
Sudut yang dibentuk oleh garis dan bidang jika garis itu sejajar atau terletak pada bidang maka sudut yang dibentuk adalah 0 derajat
Garis Tegaklurus Bidang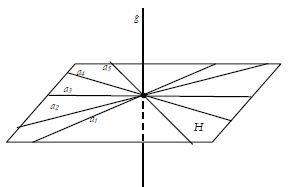
Garis a dikatakan tegaklurus bidang H, jika garis a tegaklurus pada semua garis pada bidang H yang melalui titik tembusnya.
Garis Tidak Tegaklurus Bidang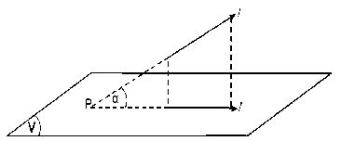
Sudut antara garis g dan bidang ∝ adalah sudut lancip yang dibentuk oleh garis g dengan proyeksi garis g tersebut pada bidang ∝.
Sudut Antara Dua Bidang (yang berpotongan)
Misalkan bidang V dan W berpotongan padagaris AB (bidang V = bidang ABCD,bidang W = bidang ABEF, sehingga (V, W) = AB ). Jika sebuah bidang K memotong tegaklurus garis potong antara bidang V dan W, maka bidang K dinamakan bidang tumpuan antara bidang V dan W. Karena bidang K ^ V dan K ^ W, maka bidang K dinamakan bidang tumpuan antara bidang V dan W. Karena bidang K ^ V dan K ^ W, maka bidang K ⊥(V, W), sehingga:diperoleh bahwa (V, W) ⊥(K, V) dan (V, W) ⊥(K, W).
Sudut antara garis (K, V) dan (K, W) dinamakan sudut tumpuan antara bidang V dan W. Besar sudut antara bidang V dan W ditentukan oleh besar sudut tumpuan antara kedua bidang.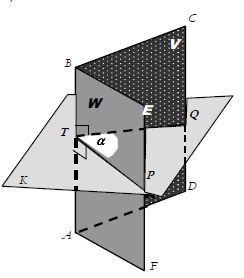
Perhatikan Gambar
Sudut yang dibentuk oleh dua bidang jika bidang-bidang tersebut saling sejajar atau berhimpit, maka besar sudut yang terbentuk adalah 0^o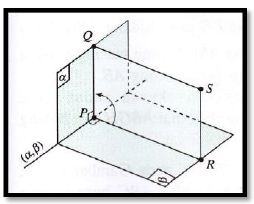
Sudut antara dua bidang yang berpotongan di garis g merupakan sudut yang dibentuk oleh dua garis yang berpotongan (sebuah garis pada bidang pertama, misalnya garis m, dan sebuah garis pada bidang kedua, misalnya garis n) garis-garis m dan n saling tegak lurus terhadap garis g.
Contoh
Hitung :
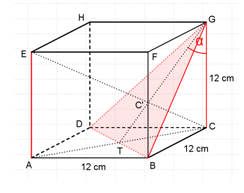
a). nilai sinus sudut antara rusuk BF dan bidang BEG
b). nilai cosinus sudut antara rusuk AE dan bidang DBG
Jawab :
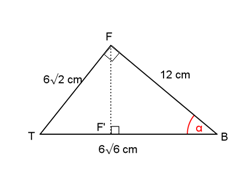
a) Cara menentukan sudut antara rusuk BF dan bidang BEG :
Kita proyeksikan titik B pada bidang BEG yaitu di titik B, kemudian proyeksikan titik F pada bidang BEG dengan cara menarik titik F ke titik D sehingga memotong bidang BEG di titik F’ (yaitu proyeksi F pada bidang BEG).
Jadi proyeksi rusuk BF pada bidang BEG adalah BF’.
Sudut antara rusuk BF dan bidang BEG adalah α = ∠GBF’ atau α = ∠GBT
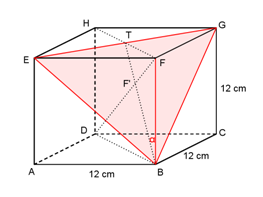
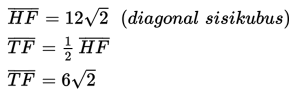
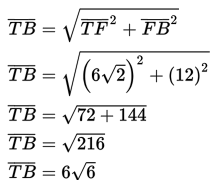
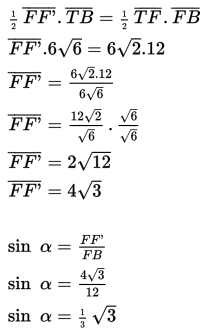
Karena rusuk AE dan bidang DBG belum berpotongan, maka AE kita geser ke CG sehingga berpotongan dengan bidang DBG di titik G.
Kemudian kita proyeksikan titik G pada bidang DBG yaitu di titik G sendiri, dan proyeksikan titik C pada bidang DBG dengan cara menarik garis dari titik C ke arah E sehingga garis memotong bidang DBG di titik C’.
Sudut antara rusuk AE dan bidang DBG adalah α = ∠CGC’ atau α = ∠CGT .