Jarak Garis ke Bidang pada Bangun Ruang

Perhatikan gambar berikut ini.

Gambar di atas merupakan sebuah bidang α dengan garis k. Kemudian garis k dan bidang α tersebut dihubungkan sebuah garis AB yang tegak lurus dengan garis dan bidang tersebut. Jarak garis AB tersebut merupakan jarak garis k dengan bidang α. Jarak garis ke bidang adalah panjang garis proyeksi garis pada bidang. Untuk memantapkan pemahaman anda tentang jarak garis ke bidang.

Contoh Soal

Perhatikan gambar kubus ABCD.EFGH di bawah ini.

 

Diketahui panjang rusuk kubus di atas 8 cm dan titik P , titik Q, titik R, serta titik S berada di tengah-tengah rusuk kubus tersebut. Hitunglah jarak garis PQ ke bidang DRS!

Penyelesaian:
Sekarang kita perhatikan gambar di bawah ini.

Perhatikan bidang DRS dan garis PQ! Garis YZ merupakan jarak antara bidang DRS dengan garis PQ di mana DX tegak lurus dengan garis YZ.  maka HX = BY = 2√2 cm, DY = 6√2 cm dan XY = 4√6 cm

Sekarang kita cari panjang DX dengan teorema Phytagoras, yaitu:

DX = √(DH² + HX²)

DX = √(8² + (2√2)²)

DX = √(64 + 8)

DX = √72

DX = 6√2 cm

Maka gambarnya menjadi:

Sekarang kita cari panjang DO dengan menggunakan teorema phytagoras, yaitu:

DO = √(DY² – OY²)

DO = √((6√2)² – (2√6)²)

DO = √(72 – 24)

DO = √48

DO = 4√3 cm

Dengan menggunakan konsep luas segitiga maka:

(DX . YZ)/2 = (XY . DO)/2
 (DX . YZ)= (XY . DO)

6√2 . YZ = 4√6 . 4√3

6√2 . YZ = 16√18

6√2 . YZ = 16 . 3√2

YZ = 16/2

YZ= 8 cm

Jadi jarak garis PQ ke bidang DRS adalah 8 cm.

CONTOH SOAL
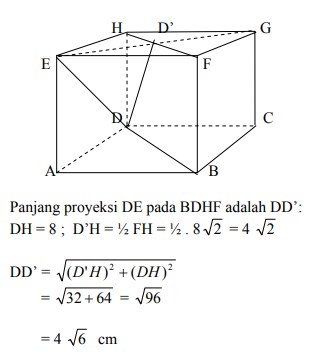
Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Tentukan panjang proyeksi DE pada BDHF 

Penyelesaian: