Setelah kita selesai mempelajari materi tentang hubungan dan
jarak antara titik, garis dan bidang, sekarang kita akan mulai
mempelajari besar sudut.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung besar sudut antara : a). AH dan HC
b). AF dan BG
c). EB dan HP
(titik P adalah perpotongan garis diagonal AC dan BD)
Jawab :
a). sudut antara AH dan HC
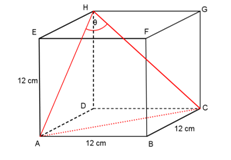 Perhatikan ΔACH
Perhatikan ΔACH
Karena AH = AC = CH = diagonal sisi kubus, maka ΔACH adalah segitiga sama sisi, sehingga ∠AHC = ϴ = 60o
b). sudut antara AF dan BG
 Garis AF dan BG bersilangan, sehingga untuk menentukan sudutnya salah satu garis harus kita geser.
Garis AF dan BG bersilangan, sehingga untuk menentukan sudutnya salah satu garis harus kita geser.
Misal AF kita geser ke DG, sehingga berpotongan dengan BG di titik G.
Jadi sudut antara AF dan BG adalah ∠DGB
Karena ΔDGB adalah segitiga sama sisi, maka ∠DGB = ϴ = 60o
c). Sudut antara EB dan HP (titik P adalah perpotongan garis diagonal AC dan BD).
 Karena EB dan HP bersilangan, maka EB kita geser ke HC sehingga berpotongan dengan HP di titik H.
Karena EB dan HP bersilangan, maka EB kita geser ke HC sehingga berpotongan dengan HP di titik H.
Jadi sudut antara EB dan HP adalah ∠PHC
Karena ΔAHC adalah segitiga sama sisi, maka ∠AHC = 60o
∠AHP = ∠PHC = ½ ∠AHC
ϴ = ∠PHC = ½ . 60o
ϴ = 30o
Sudut yang akan kita pelajari nanti adalah sudut antara dua garis, sudut antara garis dan bidang, serta sudut antara dua bidang.
Kalian masih ingat, bahwa hanya dua garis berpotongan atau dua garis bersilangan saja yang mempunyai sudut ? Sekarang kita akan mempelajari materi sudut antara dua garis baik yang berpotongan maupun yang bersilangan.
SUDUT ANTARA DUA GARIS
Sudut antara garis g dan h yang berpotongan adalah sudut yang dibentuk oleh kedua garis tersebut.
 Untuk dua garis bersilangan besar sudutnya tidak dapat langsung kita
tentukan. Cara menghitung besar sudut antara dua garis yang bersilangan
dengan cara menggeser salah garis (atau keduanya), sehingga kedua garis
berpotongan.
Untuk dua garis bersilangan besar sudutnya tidak dapat langsung kita
tentukan. Cara menghitung besar sudut antara dua garis yang bersilangan
dengan cara menggeser salah garis (atau keduanya), sehingga kedua garis
berpotongan.
Selanjutnya untuk menghitung besar sudut sama dengan cara menghitung besar sudut antara dua garis yang berpotongan.
 Misal garis g dan h bersilangan (artinya garis g dan h tidak
berpotongan), untuk menghitung besar sudutnya kita geser garis g
sehingga memotong garis h, maka sudut ϴ adalah sudut yang dibentuk oleh
g’ dan h .
Misal garis g dan h bersilangan (artinya garis g dan h tidak
berpotongan), untuk menghitung besar sudutnya kita geser garis g
sehingga memotong garis h, maka sudut ϴ adalah sudut yang dibentuk oleh
g’ dan h .
Untuk lebih jelasnya kita perhatikan contoh berikut.
Kalian masih ingat, bahwa hanya dua garis berpotongan atau dua garis bersilangan saja yang mempunyai sudut ? Sekarang kita akan mempelajari materi sudut antara dua garis baik yang berpotongan maupun yang bersilangan.
SUDUT ANTARA DUA GARIS
Sudut antara garis g dan h yang berpotongan adalah sudut yang dibentuk oleh kedua garis tersebut.

Selanjutnya untuk menghitung besar sudut sama dengan cara menghitung besar sudut antara dua garis yang berpotongan.

Untuk lebih jelasnya kita perhatikan contoh berikut.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung besar sudut antara : a). AH dan HC
b). AF dan BG
c). EB dan HP
(titik P adalah perpotongan garis diagonal AC dan BD)
Jawab :
a). sudut antara AH dan HC

Karena AH = AC = CH = diagonal sisi kubus, maka ΔACH adalah segitiga sama sisi, sehingga ∠AHC = ϴ = 60o
b). sudut antara AF dan BG

Misal AF kita geser ke DG, sehingga berpotongan dengan BG di titik G.
Jadi sudut antara AF dan BG adalah ∠DGB
Karena ΔDGB adalah segitiga sama sisi, maka ∠DGB = ϴ = 60o
c). Sudut antara EB dan HP (titik P adalah perpotongan garis diagonal AC dan BD).

Jadi sudut antara EB dan HP adalah ∠PHC
Karena ΔAHC adalah segitiga sama sisi, maka ∠AHC = 60o
∠AHP = ∠PHC = ½ ∠AHC
ϴ = ∠PHC = ½ . 60o
ϴ = 30o

No comments:
Post a Comment